GeoGebra kennen viele aus dem Einsatz im Mathematikunterricht. Auch im Physikunterricht kann das Tool sinnvoll verwendet werden. Wie das geht, zeigen wir im folgenden Artikel.
Was kann ich mit GeoGebra machen?
GeoGebra ist ursprünglich ein Geometrie-Tool. Geometrische Objekte wie Punkte, Graphen oder Funktionen können gezeichnet werden. Zusätzlich stellt GeoGebra auch eine algebraische Schnittstelle bereit, mit der Werte verändert und die Änderungen geometrisch dargestellt können.
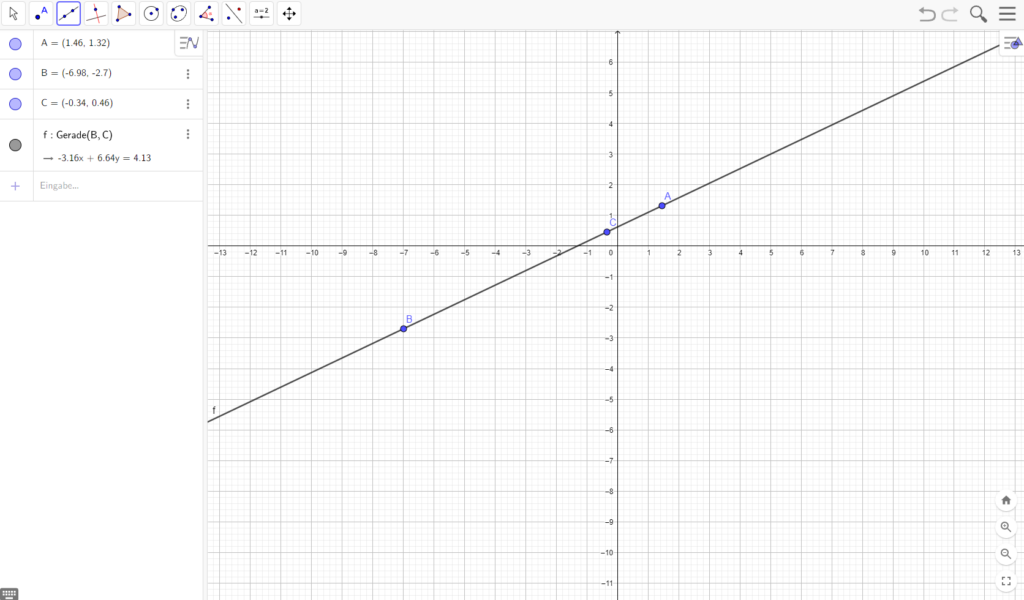
Neuere Versionen der Anwendung bietet außerdem einen CAS, können 3D-Modelle verarbeiten und verfügen über ein visuelles Werkzeug zur Darstellung von Wahrscheinlichkeiten.
Das Tool wird seit Jahren im Mathematikunterricht eingesetzt. Schüler:innen können mit GeoGebra durch das selbstständige Manipulieren von Werten explorativ mathematische Zusammenhänge erfahren. Einige Funktionen von GeoGebra für den Mathematikunterricht werden hier näher erklärt.
Das Programm steht kostenfrei für nahezu alle Plattformen bereit (Apple iOS, Android, Windows, Linux, Mac, Chromebook) und verfügt über eine recht intuitive Oberfläche.
Wie kann ich GeoGebra im Physikunterricht einsetzen?
Physikalische Gesetzmäßigkeiten können mithilfe von GeoGebra in Modellen durch Ausprobieren erfahrbar gemacht werden. Großer Vorteil ist hier, dass Schüler:innen selbst tätig werden und “sehen”, welche Folgen die Veränderungen von Parametern haben. Denkbar ist der Einsatz in vielen Phasen des Unterrichts, z.B. in der Erarbeitung einer neuen Gesetzmäßigkeit oder in einer vertiefenden Übung. Durch die einfache Bedienbarkeit der Anwendung ist auch der Einsatz in umfangreicheren selbstgesteuerten Erarbeitungen oder Lernaufgaben vorstellbar.
Die GeoGebra-Modelle, die für das Lernen im Physikunterricht benötigt werden, sind meist recht komplex. Die Benutzeroberfläche von GeoGebra ist grundsätzlich sehr übersichtlich und verständlich, sodass das Einarbeiten eigener Modelle relativ einfach möglich ist. Schritt-für-Schritt-Anleitungen für die Erstellung zahlreicher Modelle gibt es bei YouTube. Für ein Modell zur schiefen Ebene kann beispielsweise die Anleitung dieses Videos befolgt werden.
Alltagstauglicher ist es aber, auf die schon bestehenden Modelle bei GeoGebra zurückzugreifen. Professionelle Entwickler:innen, aber auch interessierte Mitglieder aus der Community haben für zahlreiche Themenbereiche bereits Modelle entwickelt. Materialien findet man leicht über die Suche auf der Seite von GeoGebra.
Nicht unerwähnt soll auch die Möglichkeit in GeoGebra bleiben, 3D-Modelle zu entwickeln und diese in einer Augmented-Reality-Umgebung einzusetzen. Das bedeutet konkret, dass physikalische Gesetzmäßigkeiten als 3D-Modell angelegt werden (z.B. Feldlinienvektoren im Feld um eine elektrisch geladene Kugel). Mithilfe von Referenzpunkten kann das Modell so auf einen tatsächlichen Versuchsaufbau “gelegt” werden. Das Modell wird in die App von GeoGebra importiert und überlagert das von der Kamera aufgenommene Bild. Neben dem eigentlichen Versuchen sehen die Schüler:innen somit auch die zugrunde liegende Gesetzmäßigkeiten. Weitere Informationen zu dieser Einsatzmöglichkeiten könnt ihr bei Albert Teichrew nachlesen, der zur Nutzung von Modellen in Experimenten an der Goethe-Universität in Frankfurt (Main) forscht. Dort findet ihr auch fertige 3D-Modelle, die ihr im Unterricht einsetzen könnt. Wie das ganze aussieht, seht ihr auch im YouTube-Video seines Kanals.
Beispiele: Einsatz von GeoGebra im Physikunterricht
Du möchtest GeoGebra gern auch in deinem Physikunterricht einsetzen? Wir haben drei GeoGebra-Modelle herausgesucht, um beispielhaft die Funktionen und Umsetzung zu zeigen. Ansonsten lassen sich, wie dargestellt, die Beispiele über die Suche bei GeoGebra finden.
Wie groß muss der Spiegel sein?
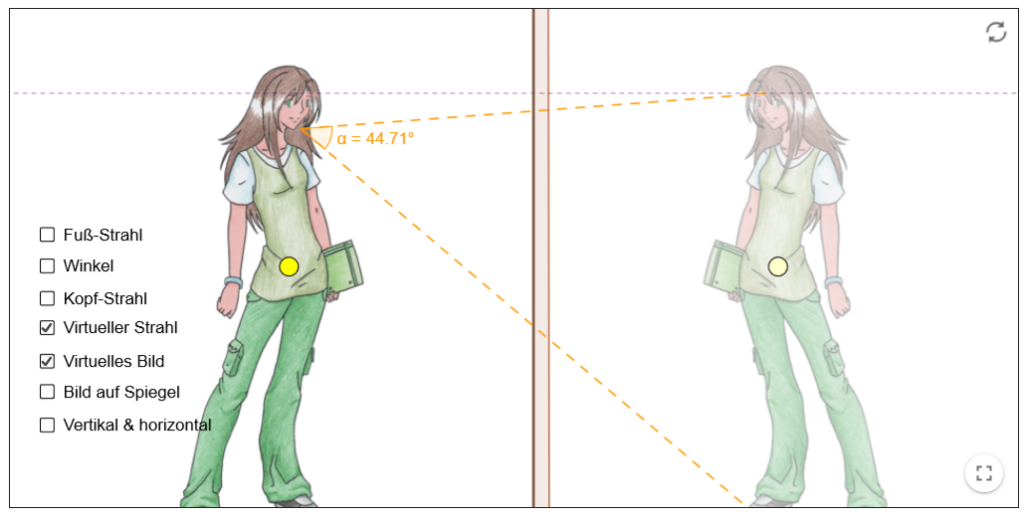
Eine übliche Aufgabe im Bereich der Optik ist die Frage danach, wie groß ein Spiegel sein muss, damit man sich in ihm vollständig sehen kann. Das Strahlenmodell und virtuelle Bilder sind für die Beantwortung der Frage wichtig. Die GeoGebra-Anwendung von Geli Delius und Markus Hohenwarter greift die Frage auf. Sie ist hier abrufbar.
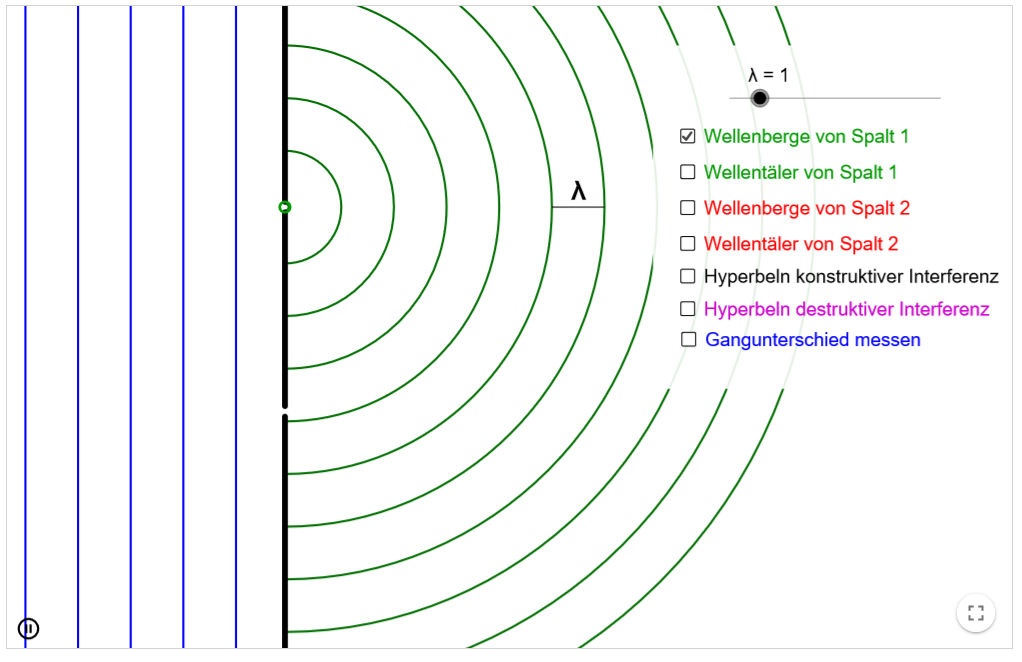
Interferenz am Doppelspalt
Wie Interferenzmuster am Doppelspalt entstehen, zeigt die folgende Simulation von C. Wolfseher. Sie ist hier abrufbar.
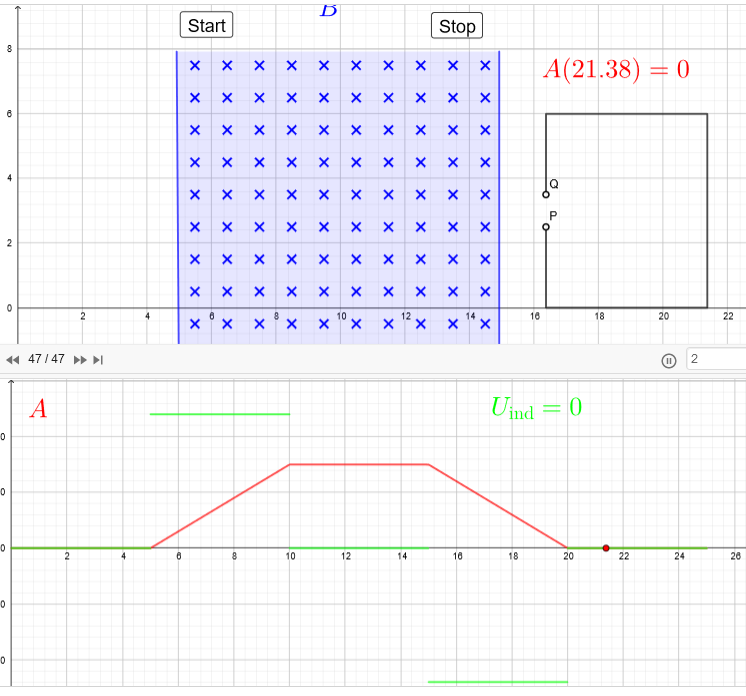
Induktion am bewegten Leiter
Ein Leiter wird durch ein Magnetfeld bewegt. Zu welchen Zeitpunkten eine Induktionsspannung entsteht, zeigt die Animation von Otto Baumann. Sie ist hier abrufbar.
Fazit
GeoGebra ist ein umfangreiches Tool, das sich gut für das “Erfahren” abstrakter Zusammenhänge eignet – nicht nur im Mathematik-, sondern auch im Physikunterricht.
Hast du bereits einige der Erweiterungen ausprobiert und möchtest von deinen Erfahrungen berichten? Erzähle uns davon in den Kommentaren zu diesem Artikel, mit einer Mail über unser Kontaktformular oder über unsere Kanäle auf Facebook, Twitter und Instagram.
Wenn dir der Artikel gefallen hat und du noch mehr lesen möchtest, findest du hier unsere anderen Beiträge.





